简介:下午茶合集11.14-11.19,可能会咕咕咕
知识点: 最小生成树, 数论, 二维矩阵二分, 构造
11.14 ABC
11.15 ABC 210E
https://atcoder.jp/contests/abc210/tasks/abc210_e
题目简介:
输入 $n(\leq 1e9)$ 和 $m(\leq 1e5)$,表示一个 $n$ 个点,$0$ 条边的图(节点编号从 $0$ 开始),以及 $m$ 个操作。
每个操作输入两个数 $a(1\leq a \leq n-1)$ 和 $c(≤1e9)$,表示你可以花费 $c$,任意选择一个 $[0,n-1]$ 内的数字 x,把 x 和 $(x+a)%n$ 连边。
这 $m$ 个操作,每个都可以执行任意多次,可以按任意顺序执行。
输出让图连通需要的最小花费。
如果无法做到,输出 $-1$。
题解
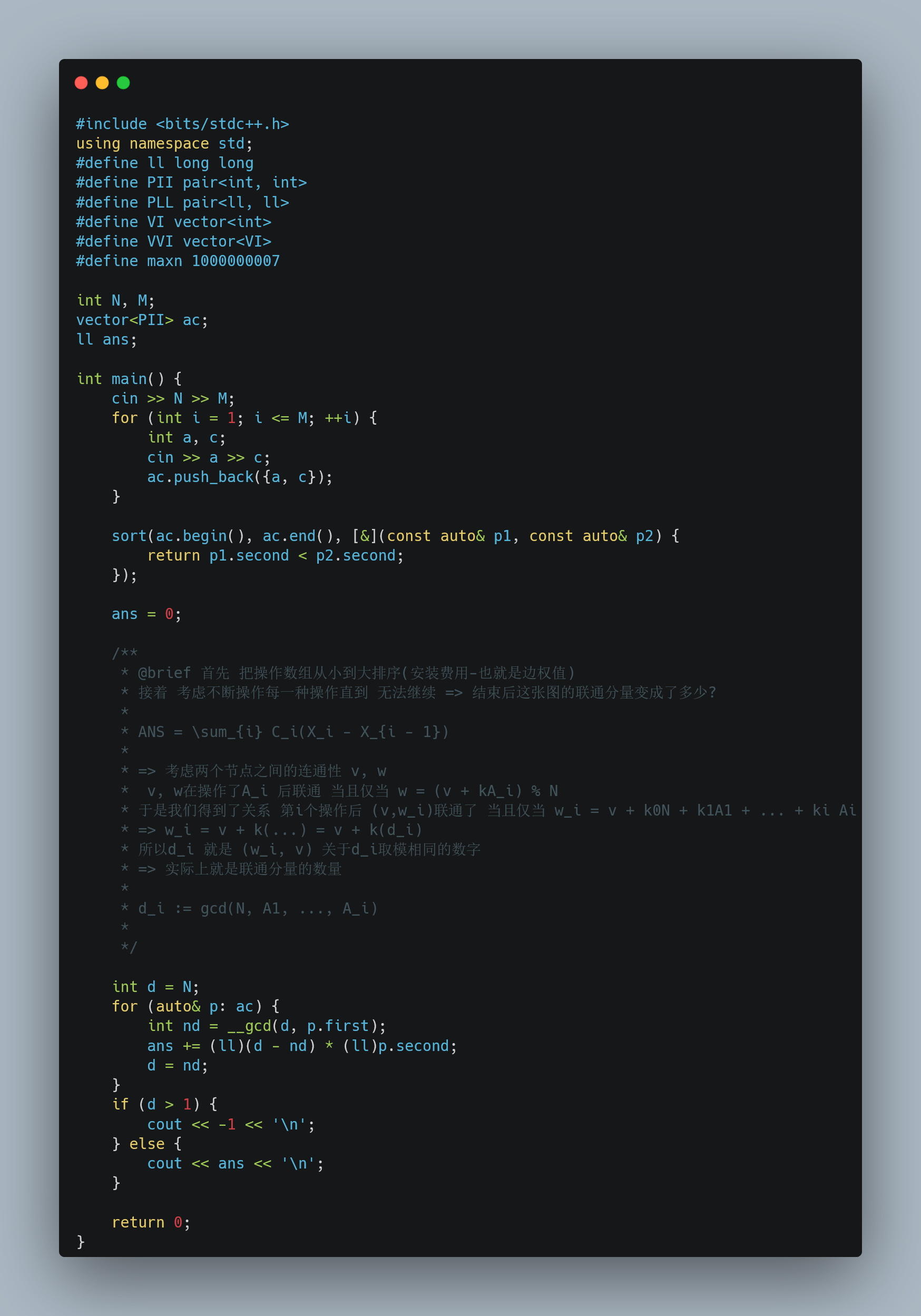
实际上就是模拟Kruskal算法寻找最小生成树的过程,但是考虑到这里这个图的边数达到了$NM$,显然不能直接使用MST算法直接求
按照cost的大小升序排序,不停的从排序后的 操作1,操作2,…开始操作
精髓在于怎么找到 “完成某些操作之后”, 连通分量的变化(这里可以发现 连通分量的数量实际上就是 约数的大小)
所以我们贪心的选取最小的代价边不断操作直到无法减少分量为止, 而这个操作次数怎么求?(实际上操作次数 == 连通分支的缩小量); 而连通分量的变化量推理后发现就是$gcd(N, A_1, …, A_n)$, 于是我们就找到了答案$\sum_{i} C_i(X_{i-1} - X_i)$, $X_i$表示用完第$i$个操作后连通分量的数量
https://atcoder.jp/contests/abc210/editorial/2307
11.16 ABC 203D
https://atcoder.jp/contests/abc203/tasks/abc203_d
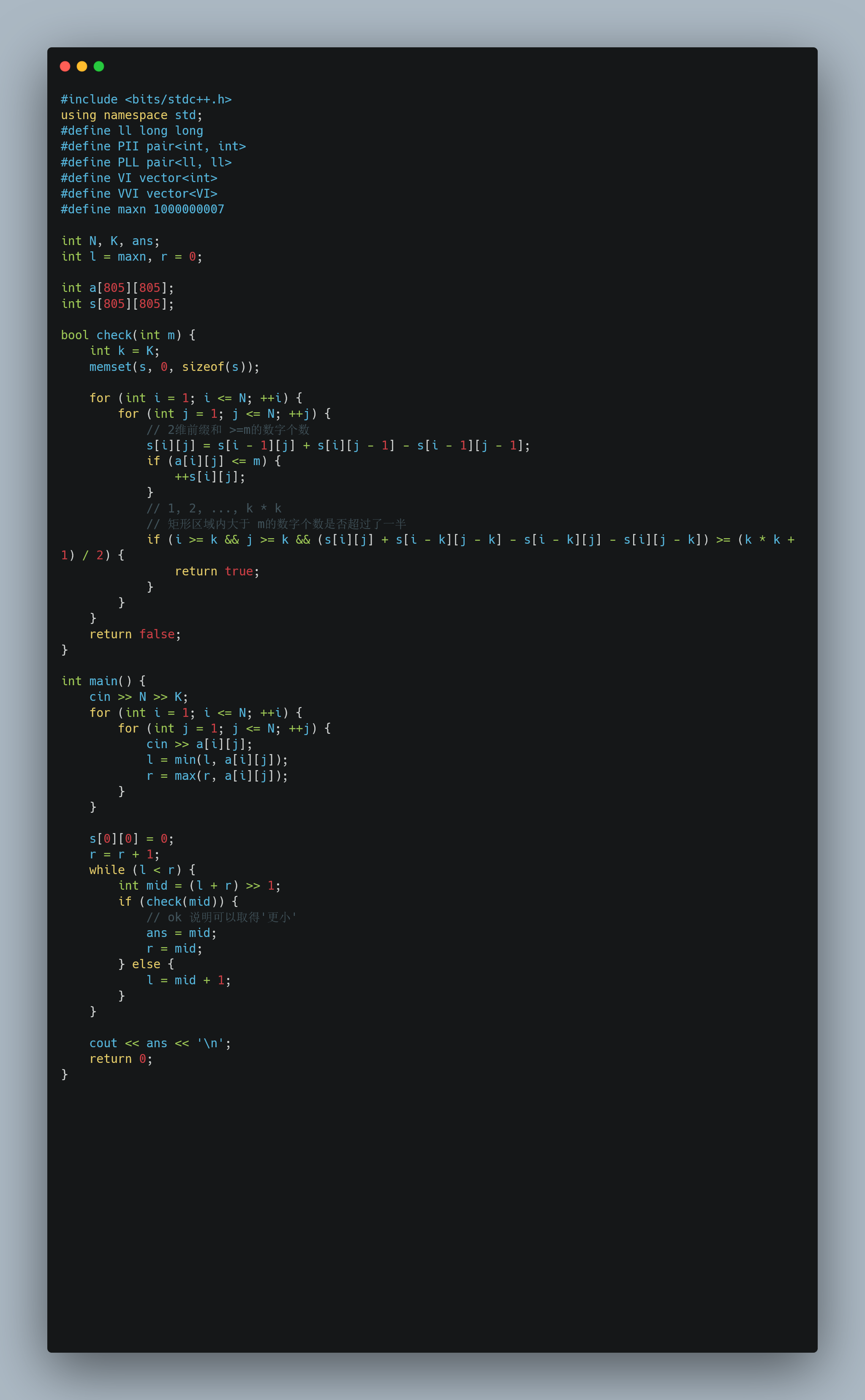
题目简介: 对于一个$N\times N$的矩阵, 给定大小$K$, 找到所有$K\times K$的子矩阵中的中位数中最小的元素(即所有子矩阵中位数的最小值)
题解
二分答案(子矩阵最小值) $logU$, 观察是否可以取到;
对于一个矩形区域, 如何快速得知 小于等于某一个数$x$的元素个数?
二维区域的前缀和($N^2$的复杂度进行维护)
算法总复杂度$N^2logU,\ U = 1e9$