下午茶知识点: 二维前缀和, 贪心&构造, 双指针&找规律
11.21 106D AtCoder Express 2
https://atcoder.jp/contests/abc106/tasks/abc106_d
11.22 178F Contrast
https://atcoder.jp/contests/abc178/tasks/abc178_f
找众数, A+B数组中出现超过了N次 => 不可能实现, No;
否则一定可以!(具体怎么构造?)
输入按照升序排列, 构造的时候刻意逆序(这样可以尽可能避免相同)
如果还是相同了! 从前往后遍历, 就从前面换(前面的至少大于等于)
由于之前的保证, 我们肯定有解, 所以不会死循环
11.23 C - Swaps 2
https://atcoder.jp/contests/arc120/tasks/arc120_c
a和b最终如果可以经过操作相等
a[1], …, a[n]
左移x次 变成 a[i] + X
右移X次 变成 a[i] - X
如果最终 a[i]和b[j]匹配, 那么 $a[i] + p - q = b[j]$ 成立
$a[i] + i == b[j] + j$成立(不太清楚怎么能够推出来的…)
通过相邻交换数组a’ 变成b’所需要的最小操作次数(等价于求逆序对数量)
记录a数组内所有元素及其对应位置(对于相同元素: 从小到大)
遍历b数组, 观察当前b数组的值v在a中出现的位置
- 如果不存在 说明不可能实现 返回-1
- 否则, 从a中对应元素的位置中取出第一个位置j, 当前位置为i
- 那么邻项交换这一段的代价就是[j, i]这一段的逆序对数量
- 使用树状数组维护逆序对数量..
11.24 133C - Row Column Sums
构造题
给定a, b数组, 构造一个矩阵满足
第i行的和 % K= a[i]第j列的和 % K= b[j]
矩阵元素取值范围为 $[0, K - 1]$
如果可以做到, 给出矩阵的最小元素和, 否则输出-1
初始化这个矩阵如下: 全部填最大, 然后逐渐缩小
$$
\begin{bmatrix}
k-1 & k-1\
k-1 & k-1
\end{bmatrix}
$$
对于第$i$行的元素, 需要减小$((k-1)\times m - a[i]) % k$
对于第$j$列的元素, 需要减小$((k-1)\times n - b[j]) % k$
证明至少要减小$Z=max(\sum_i C_i, \sum_j D_j)$, 且不会出现负数.
$(\sum_{1\leq i \leq H} C_i) \ mod\ K = (\sum_{1\leq j \leq W} D_j) \ mod\ K$
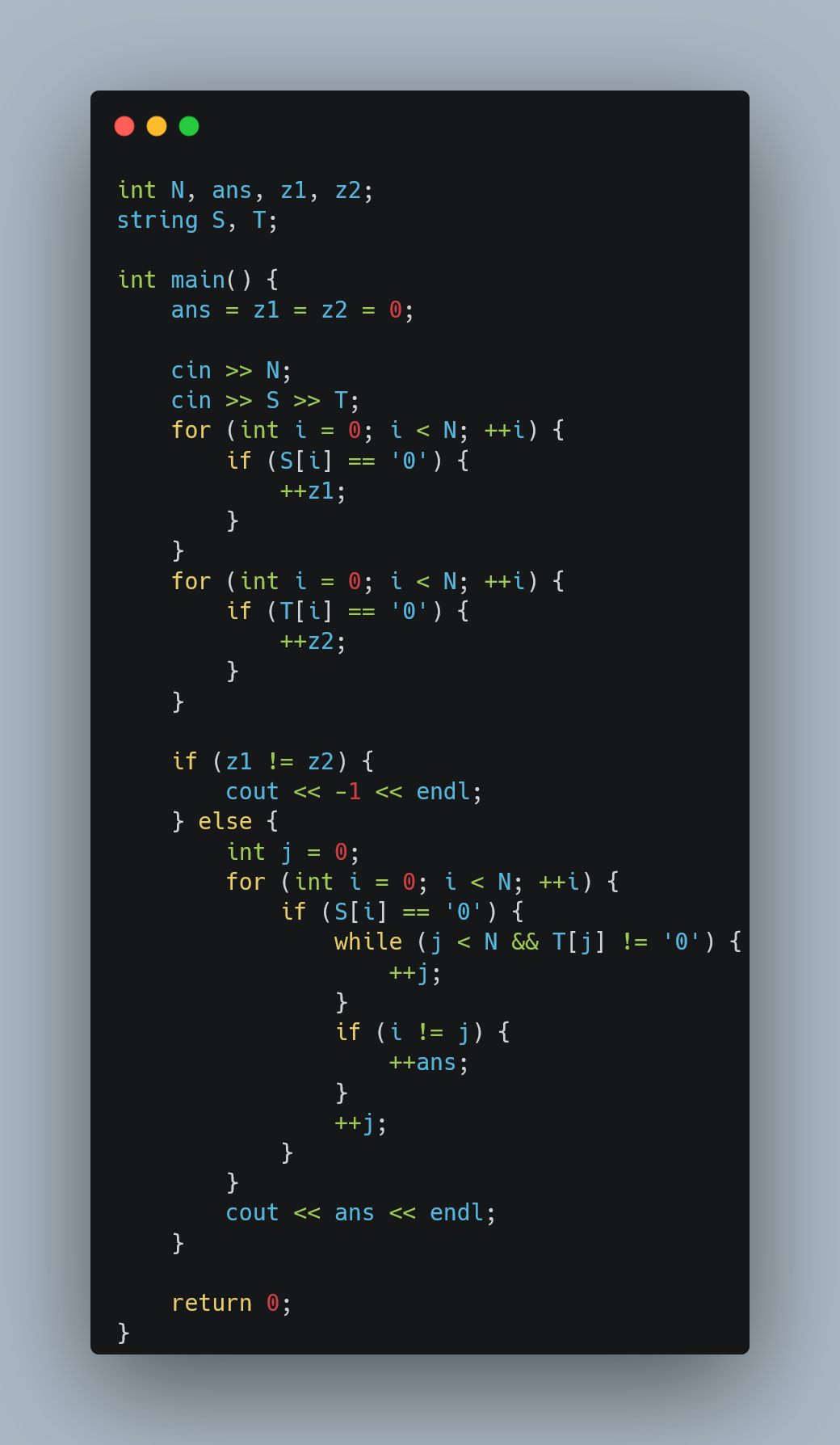
11.25 119B - Electric Board
https://atcoder.jp/contests/arc119/tasks/arc119_b
题中给到的交换操作只限于
- 交换0(1)+的 最左侧&最右侧字符 变成 11111…0的形式
- 交换1(0)+的 最左侧&最右侧字符 变成 10000…0的形式
重要性质:
- 不会对0的数量产生影响
- 对于已经在对应位置上的0 我们不需要交换 否则说明需要
假设S中的0位置为 i1, T[i1] = 1说明需要交换
- 交换给谁?
证明一下发现按照相对位置顺序交换是最优的, 为什么?
- S中相邻的两个0, 位置为$i_1, i_2$, 且满足$i_1 < i_2$
- T中相邻的两个0, 位置为$j_1, j_2$, 且满足$j_1 < j_2$
如果不对应顺序 => 交换必然导致 $i_1\to j_2$, $i_2 \to j_1$ 这种情况发生
- 而 $i_1 \to j_1$, $i_2 \to j_2$ 的代价更小(没有重叠段)
所以只需要按照顺序依次求出0位置的差值即可.