下午茶合集-1205

下午茶合集，这周的重点感觉就是各种排列问题，以及构造（太难了）

1205 ARC 100B Equal Cut

https://atcoder.jp/contests/abc102/tasks/arc100_b

输入$n(4\le n \le 1e5)$ 和一个长为 $n$ 的数组 $a (1\le a[i] \le 1e9)$

将 $a$ 分割成 $4$ 个非空连续子数组，计算这 $4$ 个子数组的元素和。
你需要最小化这 4 个和中的最大值与最小值的差，输出这个最小值。

提示：

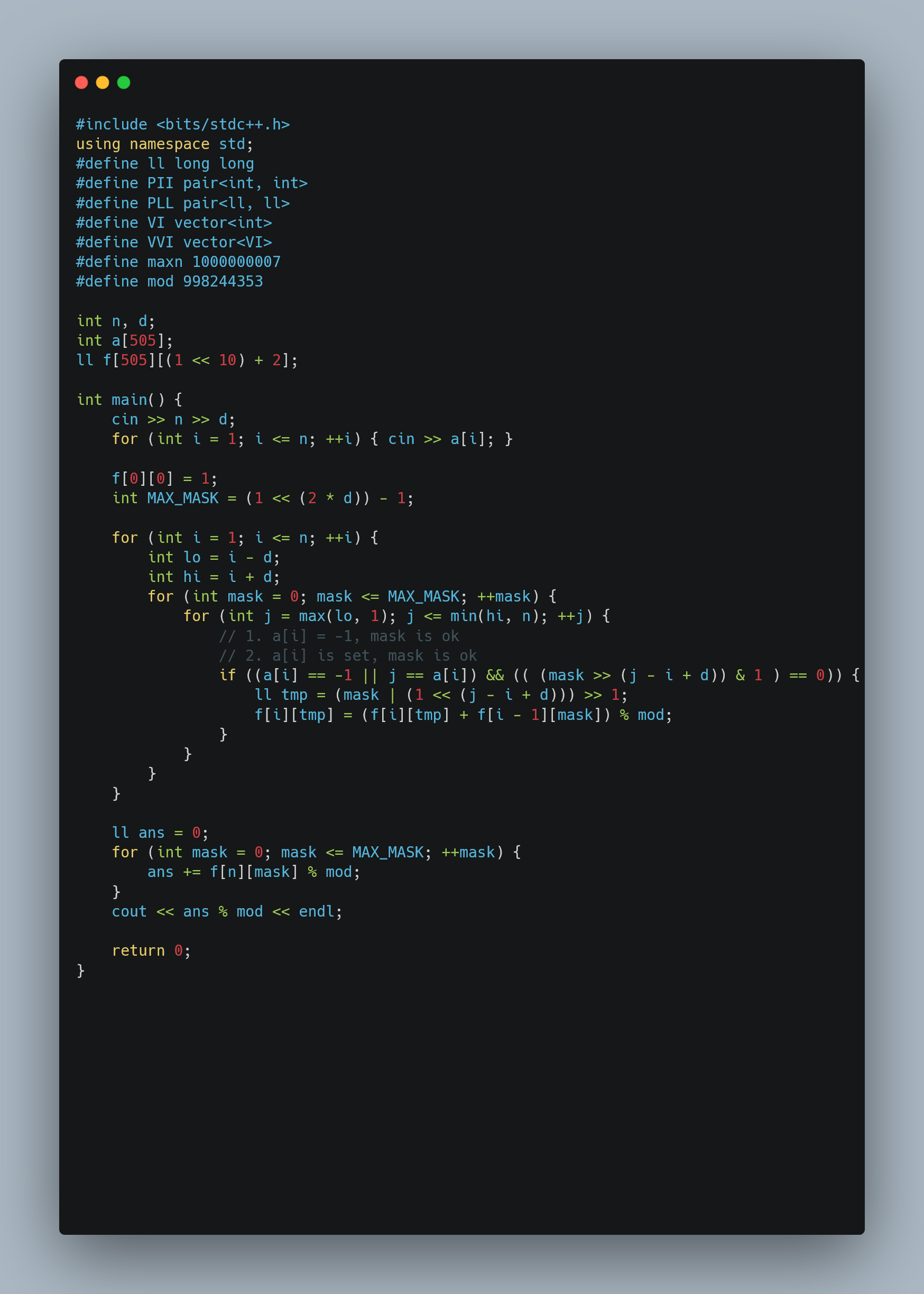
如果只划分2个区域，如果只增加其中一个区域，必然会使得一个区域变得更小，那么就一定让差值变大！所以需要尽可能均匀划分。
4个区域等价于切3刀，那么至少需要维护这三个位置，区间和可以用前缀和来计算。

枚举中间位置，那么剩余两刀总是希望切的尽可能均匀（原因在上面的例子中给出了），那么当我们向右移动中间指针，剩余的两个划分也应该向右（这样保证了我们的算法是$O(N)$的）

1207 ARC 140C

https://atcoder.jp/contests/arc140/tasks/arc140_c

脑筋急转弯的构造题
上升下降子序列的变形, 构造具有一定的规律
总是希望数字可以尽可能的被用到, 且我们可用的只有排列的$1-N$, 而差值需要严格递增
容易想到构造
$$
X, X-1, X+1, X-2, X+2,…
$$
这种
或者是
$$
X, X+1, X-1, X+2, X-2,…
$$
这一种结构

参考实现（比较简单）

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define VI vector<int>
#define VVI vector<VI>
#define maxn 1000000007
#define mod 1000000007

int N, X;
vector<int> v;

int main() {
    cin >> N >> X;
    for (int i = 1; i <= N; ++i) {
        if (i != X) { v.push_back(i); }
    }

    if (N % 2) {
        --N;
        N /= 2;
        cout << X << ' ';
        for (int i = 0; i < N; ++i) {
            cout << v[N - 1 - i] << ' ';
            cout << v[N + i] << ' ';
        }
    } else {
        if (X == N / 2 || X == N / 2 + 1) {
            // 特判
            int sgn = 1, cur = X;
            if (X == N / 2 + 1) { sgn = -1; }
            
            for (int j = 1; j <= N - 1; ++j) {
                cout << cur << ' ';
                cur += sgn * j;
                sgn = -sgn;
            }
            cout << cur << ' ';
        } else {
            cout << X << ' ';
            --N;
            N /= 2;
            for (int i = 0; i < N; ++i) {
                cout << v[N - i] << ' ';
                cout << v[N + 1 + i] << ' ';
            }
            cout << v[0] << ' ';
        }
    }

    return 0;
}

1208 ARC 144C K Derangement

寻找字典序最小的排列，满足条件$|A_i - i| \geq K, \forall\ i(1\leq i \leq N)$

$2 \leq N \leq 3 \times 10^5 $
$1 \leq K \leq N - 1$

题解：

首先可以发现$K$的大小有限制，$N \ge 2K$时才有可能有解。
贪心：如何得到最小字典序的排列？

一个错误的贪心算法：每一轮操作从满足$|x-i| \geq K$的最小数字中拿一个。

当构造排列时，对于每个下标i，需要设置$A_i$;但是由于$A_i$是一个排列，每个数字都只出现一次，需要额外考虑一些条件（即可能出现贪心的选取导致后续再也去不了的情况出现）

例如：

8 3

前三个数字，根据要求我们可以取4 5 6
第4个数字满足$|x - 4| \geq 3$所以$x = 1$或者$x \geq 7$; 理论上我们可以取1，如果我们确实拿了1，就会变成4 5 6 1

第5个数字只能取 8，第6个数字只能取 3，第7个数字只能取 2，此时我们发现剩下的是7，但是不满足要求，所以第8个数字就没有数字可以取了，说明我们并不能取1.

一个正确的贪心算法：
对于i = 1,2,3,…

如果 j = i + K 不在之前的序列中出现过，并且 j > N - K，那么取Ai = j
否则，始终选满足$|x - i|\geq K$的最小未出现数字，加入序列。

为什么这个算法是正确的？

分类讨论：
对于$2K \leq N \leq 4K$

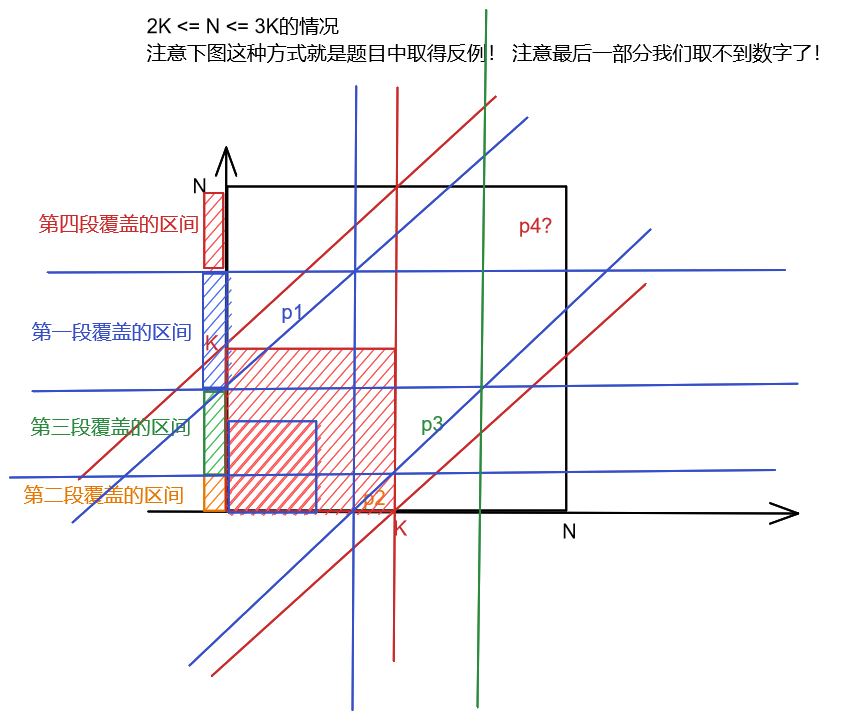
对于$2K\leq N \leq 3K$
可以按照这样的方式构造答案(以$N-K$为分界点)

贴一个错误的贪心：

$$ A_i = \begin{cases} i + K,\ i \leq N - K \\ i + K - N,\ N - K + 1\leq i \leq N \\ \end{cases} $$

正确的贪心结果：

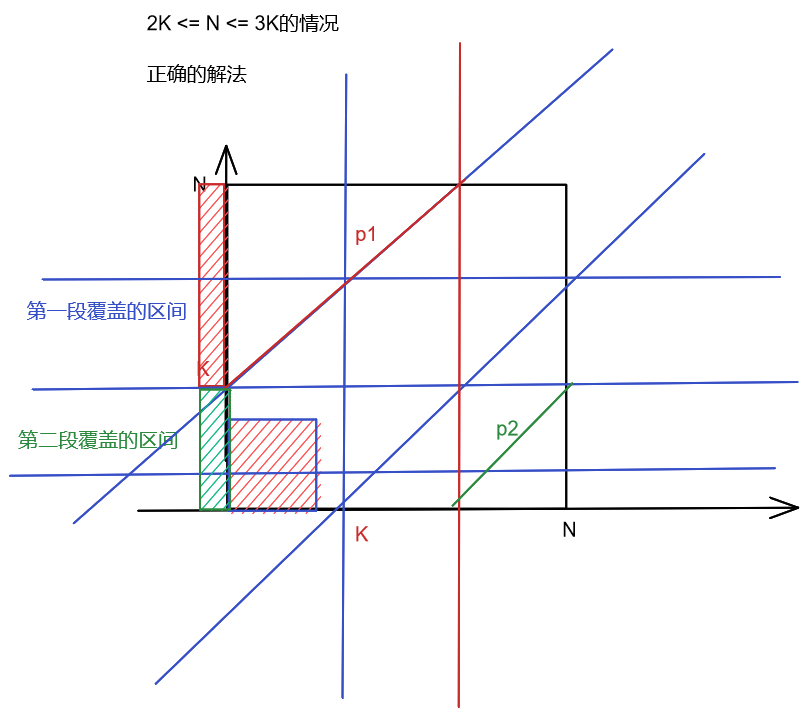
比较复杂的是对于$3K\lt N \leq 4K$的情况

这个时候的$N - K$大于$2K$了，不能用上面一样的式子(否则会有重复的值出现)

$$ A_i = \begin{cases} i + K,\ i \leq K \\ i - K,\ K \lt i \leq N - 2K \\ i + K,\ N - 2K \lt i \leq N - K \\ i + K,\ N - K \lt i \leq 3K \\ i - K,\ 3K \lt i \leq N \\ \end{cases} $$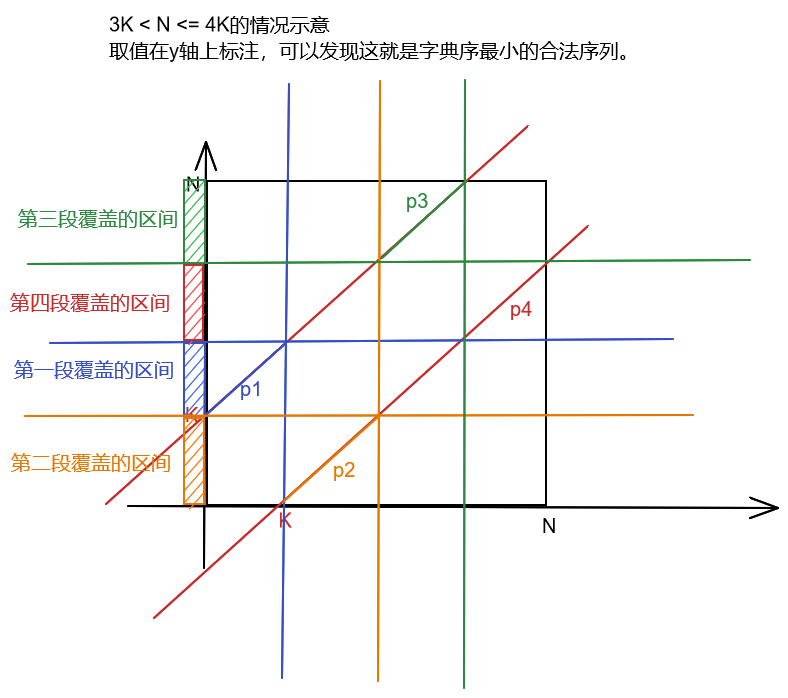

对于$N\geq 4K$的情况：
我们可以输出$(K+1,…,2K, 1,…,K)$作为前$2K$项的结果，剩余的$N-2K$项由上面的两类情况给出答案，从而满足要求。

难点：实现代码，多种情况

1209 ARC 132C Almost Sorted

https://atcoder.jp/contests/arc132/tasks/arc132_c

输入 $n(\lt 500)$, $d(\lt 5)$ 和长为 $n$ 的数组 $a$。
$a$ 原本是一个 $1~n$ 的排列 $p$，不过有些数字被替换成了 $-1$。
你需要还原 $p$，使得 $abs(p[i]-i) \lt d$ 对每个 $i$ 都成立。
输出有多少个这样的 $p$，模 $998244353$。

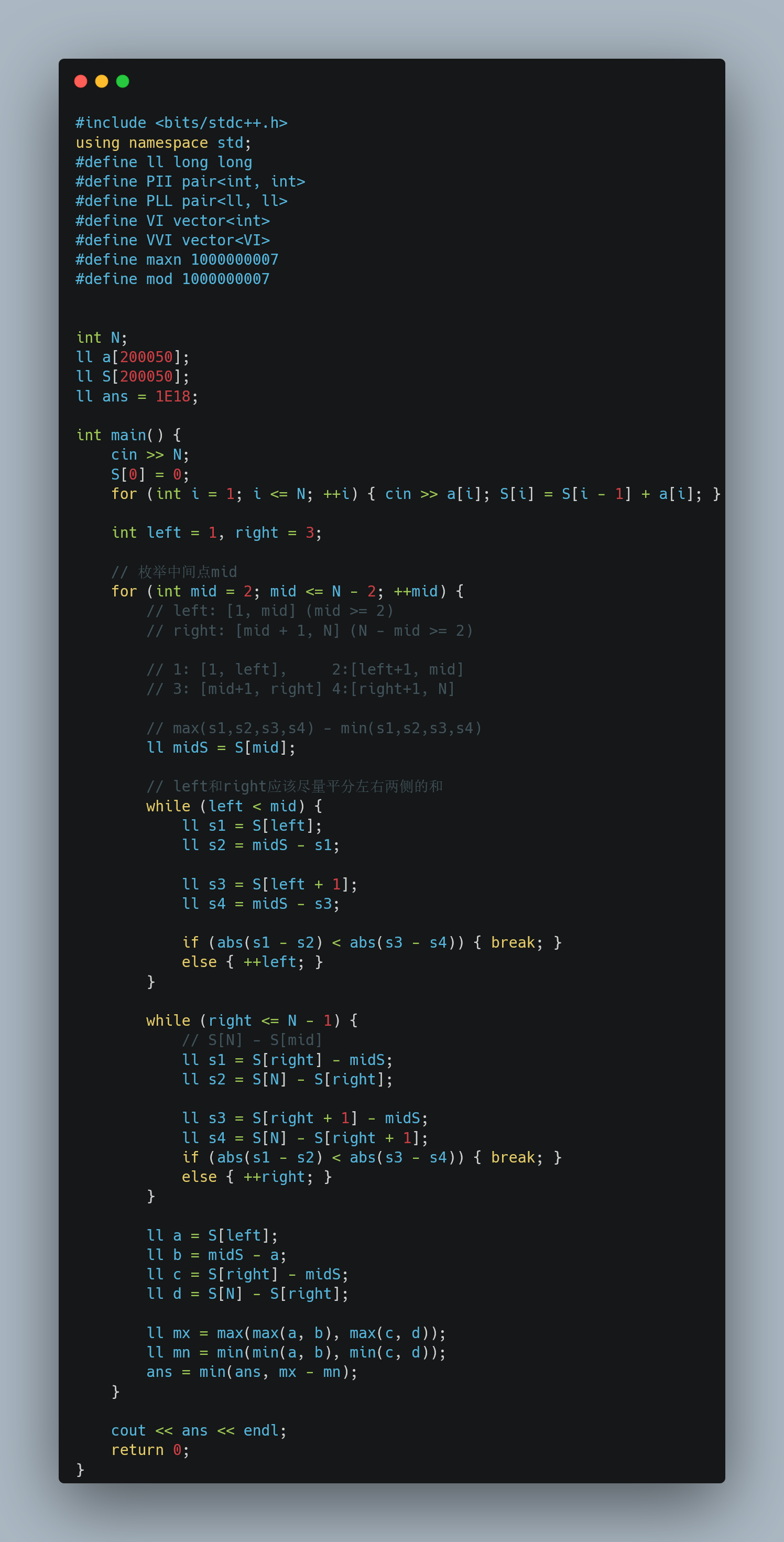
题解：
枚举每一位上放什么数字，根据题目限制，实际上可行的数字范围只有2d这么多个，因此用一个2d位长的bit-mask就可以完成状态的表示了。

Q：是否存在重复表示的问题？
A：不存在，重复使用的数字会体现在之前位置上的bit-mask状态中，因此在后面的位置上，如果可以从前一个状态转移而来一定是合法的。

参考代码