构造与贪心
12.12 ARC 147B
https://atcoder.jp/contests/arc147/tasks/arc147_b
输入 $n(\leq 400)$ 和一个 $1-n$ 的排列 $p$, 下标从 $1$ 开始。
你有两种操作:
操作 “A i” 可以交换 p[i] 和 p[i+1] ;
操作 “B i” 可以交换 p[i] 和 p[i+2]。
你需要让 $p$ 变为递增的。
最小化操作 $A$ 的次数,同时总操作次数不能超过 $1e5$。
输出总操作次数,以及具体的操作内容,详见样例。
如果有多个符合要求的方案,输出任意一种。
保证存在这样的操作方案。
注意到B操作不会改变元素下标的奇偶性,因此无论B操作运用多少次都没办法消除相邻的逆序对, 我们可以通过B操作把元素按照奇数下标序列, 偶数下标序列的方式进行排序(这是肯定可以做到的,次数的上限就是2 * 200 * 200 = 40000次)
然后这里还会存在相邻元素之间的逆序关系
奇数下标序列: $p_1, p_3, …, p_{2k+1}$
偶数下标序列: $p_2, p_4, …, p_{2k+2}$
此时我们再用A操作交换即可, 次数也至多只有400次; 最后就可以得到答案.
12.13 ARC 125C
https://atcoder.jp/contests/arc125/tasks/arc125_c
输入 $n, k (k\leq n \leq 2e5)$ 和一个长为 $k$ 的严格递增数组 $a$,元素范围 $[1,n]$。
输出一个 $1-n$ 的排列 $p$,使得 $a$ 是 $p$ 的一个 $LIS$。
如果有多个这样的 $p$,输出字典序最小的那个。
注:LIS 指最长上升子序列。
先考虑LIS的构成, $x_1,…,x_k$
首先我们的序列肯定要包含这些元素, 接着不能够让LIS变得更长
所以, 比$x_k$还要大的元素 要么放在最前面, 但是这样会使得字典序排序很大, 要么就预留最后一个元素$x_k$放在最后面, 中间把这些元素倒序排列, 这样可以让字典序排序更靠前一点.
解决完这些元素之后, 为了使得字典序最小, 需要尽可能地把小元素插入间隙中, 这一点可以直接通过一个指针完成, 每次考虑插入比当前已经放入元素更小, 但是还没有被使用地数字.
12.14 ARC 91C
https://atcoder.jp/contests/arc091/tasks/arc091_c
输入 $n, a, b(\leq 3e5)$
构造一个 $1-n$ 的排列,其 LIS 的长度为 $a$,LDS 的长度为$b$。
如果不存在这样的排列,输出 $-1$, 否则输出任意一个满足要求的排列。
注:LIS 指最长上升子序列, LDS 指最长下降子序列。
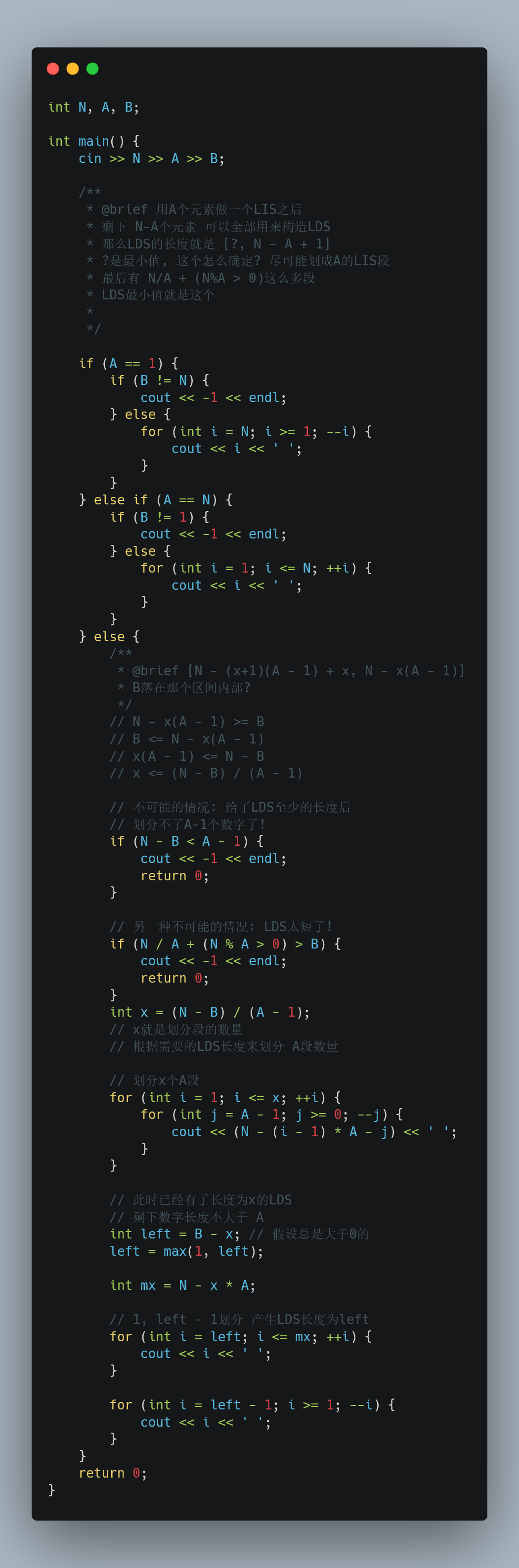
可以选择其中的一种序列进行构造, 例如长度为$a$的LIS, 可以构造成$X_1= 1,2,3,…,a$, $X_2=a+1,a+2,…, 2a$这样的片段, 然后组成$X_2, X_1$这样的排列就可以构造出LDS = 2的下降子序列了.
大致的实现方式就是这样的, 具体在实现是可以通过最终剩下元素的数量直接判断是否可能达成LDS/LIS的构造, 提前结束.
贴一个实现:
12.15 keyence2020 D
https://atcoder.jp/contests/keyence2020/tasks/keyence2020_d
输入 $n \leq 18$ 和两个长为 $n$ 的数组 $a, b$,元素范围在 $[1,50]$
$a[i]$ 和 $b[i]$ 表示第 $i$ 张牌的正面数字和背面数字。
初始所有牌正面朝上。
每次操作你可以交换第 $i$ 和 $i+1$ 张牌的位置,同时翻转这两张牌
输出让看到的数字从左往右是递增(允许相等)所需要的最小操作次数。
如果无法做到,输出 $-1$
12.16 ABC 214E
https://atcoder.jp/contests/abc214/tasks/abc214_e
输入 $t(\leq 2e5)$ 表示 $t$ 组数据,每组数据输入 $n(\leq 2e5)$ 和 $n$ 个区间 $[L,R]$,范围在 $[1,1e9]$
所有数据的 $n$ 之和不超过 $2e5$
你有 $n$ 个球,第 $i$ 个球需要放在区间 [L,R] 内的整数位置上, 但每个整数位置上至多能放一个球;
如果可以做到, 输出 Yes, 否则输出 No
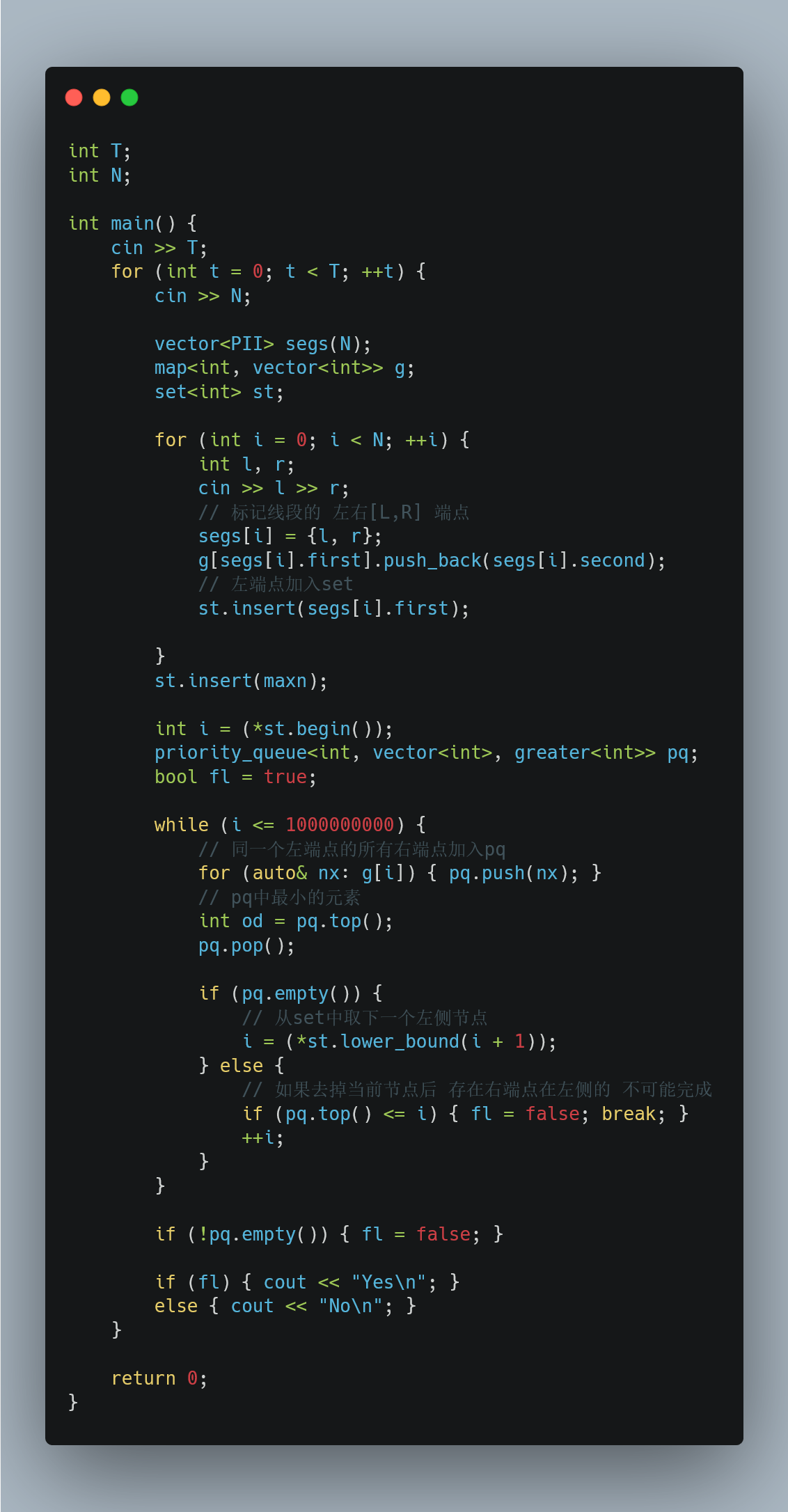
每个整数位置上只能放一个球, 所以需要合理安排这个球所对应的区间, 让它尽可能满足那些更难以被靠后的位置满足的区间, 这样看起来是最好的.
所以, 这样就可以想到贪心的做法, 首先排序这些区间(升序), 然后对于左端点相同的区间, 我们排序它们的右端点, 右端点最小的优先被我们考虑放球
如果此时这一系列区间都被处理完了, 可以直接(放到左端点)
否则放在这个端点上面, 并且与 此时放球的指针位置 进行比较, 如果当前这个区间在左侧, 说明不可能完成了, 直接退出; 否则就在这个位置上模拟放球, 增加指针
不断重复这样的操作, 直到所有的区间被处理完成或者是无法完成中途退出.
实际的实现中用一个set来维护我们的放球位置, 首先初始化为所有的左端点+哨兵maxn