补档ing
12.19 ABC 272E
https://atcoder.jp/contests/abc272/tasks/abc272_e
输入 n(≤2e5) m(≤2e5) 和长为 n 的整数数组 a (-1e9≤a[i]≤1e9),下标从 1 开始。
执行如下操作 m 次:
对 1~n 的每个 i,把 a[i] += i。
每次操作后,输出 mex(a),即不在 a 中的最小非负整数。
可以知道的一点是mex(a)这个答案的范围一定在$[0,N-1]$之内, 因为假设我们操作很多次之后所有位置上的数字都会变得很大, 由于只有N个数字, 根据鸽笼原理, 至多覆盖从$0$开始的N个位置, 那么如果让最小的那个数字超过了0, 答案就可以取到0, 依次类推, 最终可以发现答案取值是有一个很小的范围的.
那么我们对于每个位置上的数字进行累加次数的讨论, 感兴趣的只有:
- 累加L次后, 这个数(如果是负数)刚好大于0了
- 累加R次后, 这个数刚好超过(大于等于N)了
那么在$[L,R]$区间内部的累加次数, 这个位置上的数字就处于影响范围内, 需要被考虑; 我们就根据这样的方式按照累加次数进行归类, 每次都来验证一下哪个数字没有出现在$[0,N-1]$的范围内
- (为什么不会超时?)
- 第一个数字+1, 累加次数至多N次, 出现N次
- 第二个数字+2, 累加次数至多N/2次, 出现N/2次
- … 一直到第N个数字+N, 只会加N/N=1次, 出现1次
$\sum_{i=1}^N \frac{N}{i}$这个级数的模糊上界至少是$N \times log(N)$的, 因此不用担心暴力验证会出现超时的问题(循环内部的执行操作次数最多只有NlogN次).
12.20 ABC 266F
https://atcoder.jp/contests/abc266/tasks/abc266_f
输入 n (3≤n≤2e5) 和 n 条边,点的编号在 [1,n] 内,表示一个没有重边和自环的无向连通图。
然后输入 q(≤2e5) 表示有 q 个询问,每个询问输入两个数 x 和 y (1≤x<y≤n)。
对于每个询问,如果 x 和 y 之间只存在唯一的简单路径,则输出 Yes,否则输出 No。
没写, 等填坑, 基环树
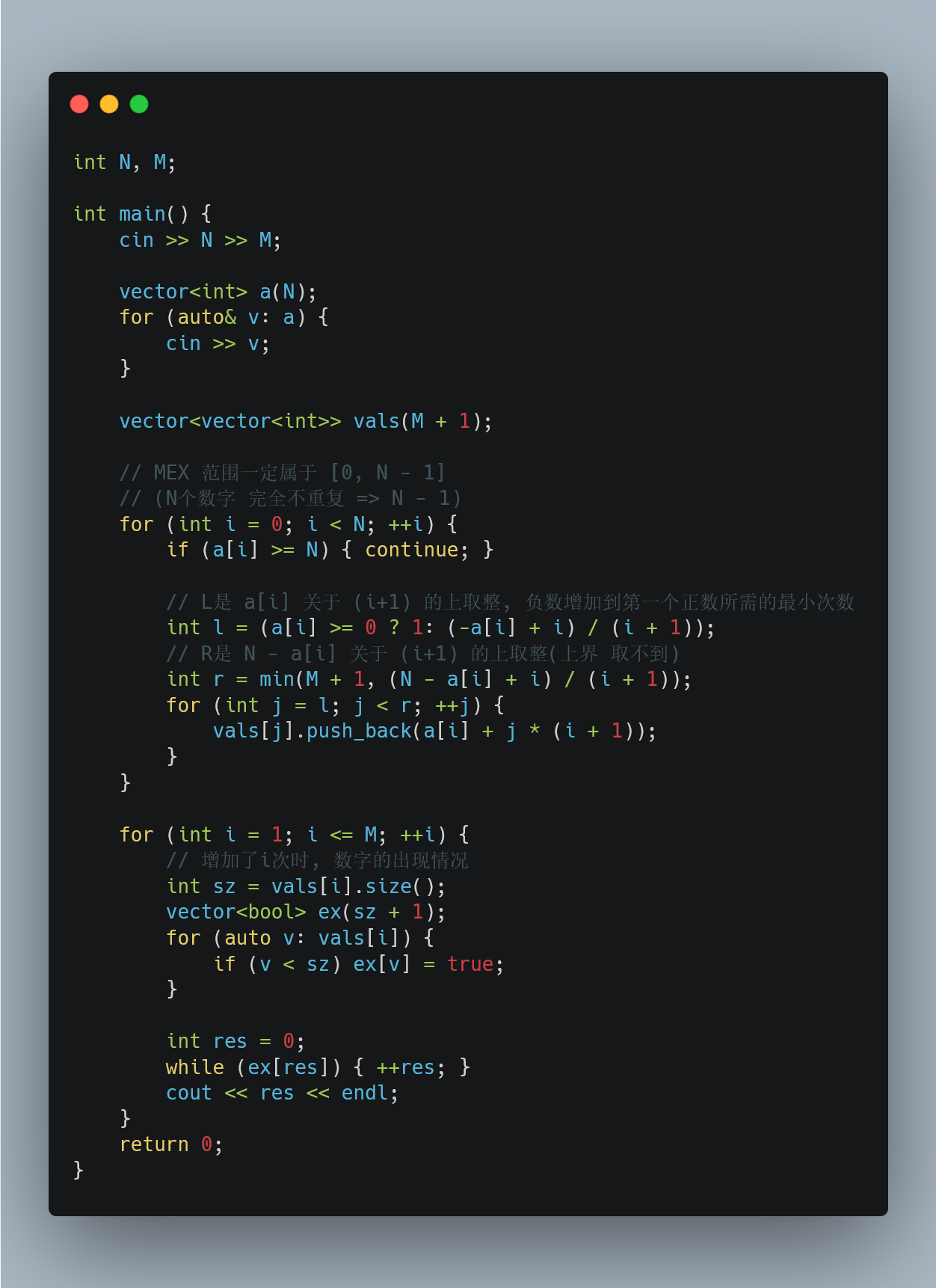
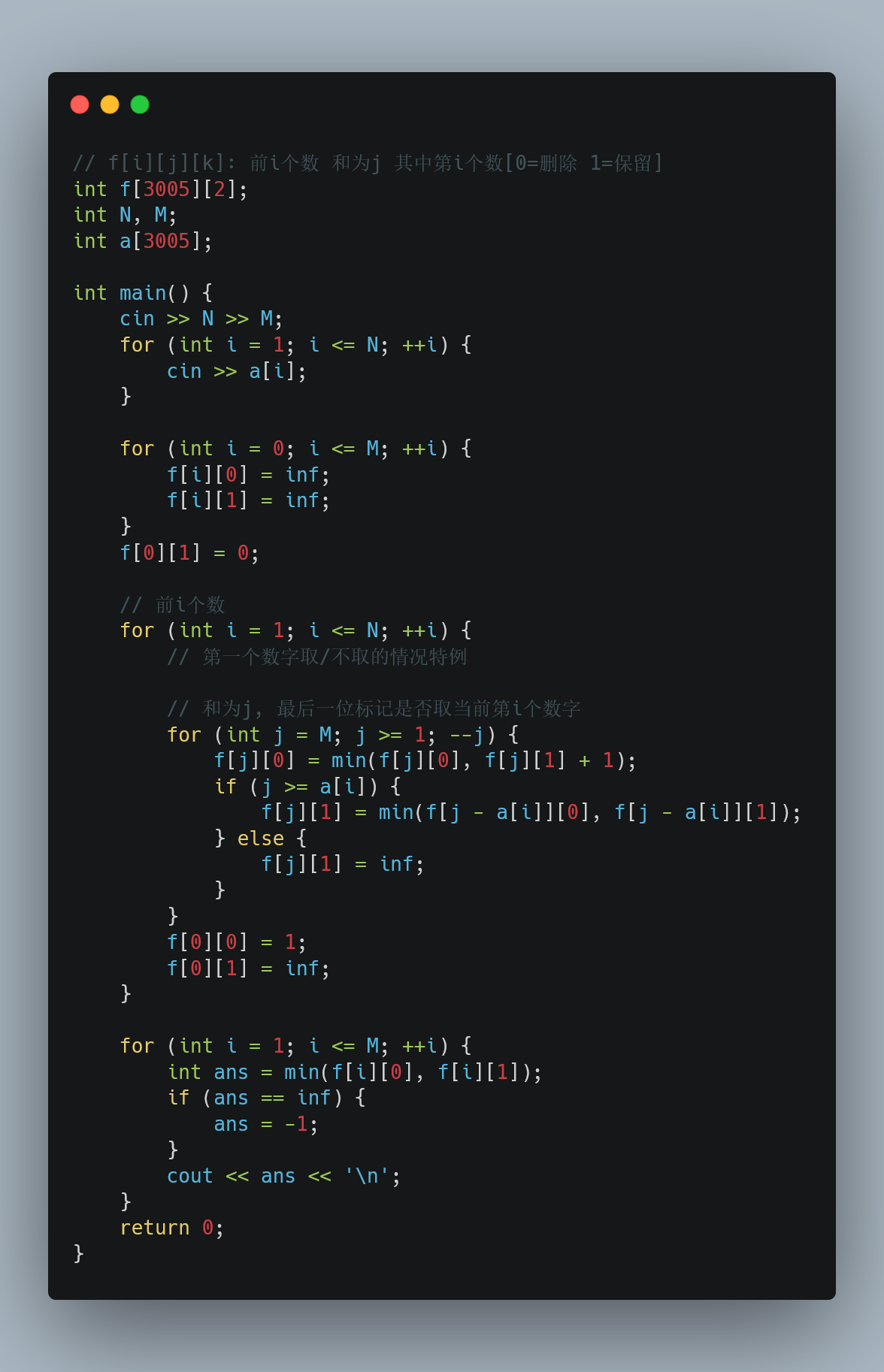
12.21 ABC 275F
https://atcoder.jp/contests/abc275/tasks/abc275_f
输入 $n(\leq 3000) m(\leq 3000)$ 和长为 $n$ 的数组 $a (1\leq a[i] \leq 3000)$。
每次操作你可以删除 $a$ 的一个非空连续子数组。
定义 $f(x)$ 表示使 $sum(a) = x$ 的最小操作次数。
输出 $f(1), f(2), …, f(m)$
构造一个系数数组$b[n]$
那么当我们选取某个$a[i]$的时候, 对应$b[i] = 1$, 否则$b[i] = 0$, 表示不取$a[i]$
考虑$S = \sum_{i=1}^N a[i]b[i] $, 当$S = x, x\in [1, m]$时, 等价于求出了原问题的一种操作方式
定义$f[S][0/1]$表示前?个数字, 取和为$S$, 最后一个数字取or不取的最少操作数.
类似于0-1背包问题, 我们发现:
- 当前和为S, 这个数不取的情况, 等于之前取+不取(删除, 1次) $f[S][0] = min(f[S][0], f[S][1] + 1)$
- 当前和为S, 如果这个数可以取 $f[S][1] = min(f[S - x][0], f[S - x][1])$ , 否则$f[S][1] = inf$
最后返回 $S = 1 - M$ 的所有情况解的值即可.
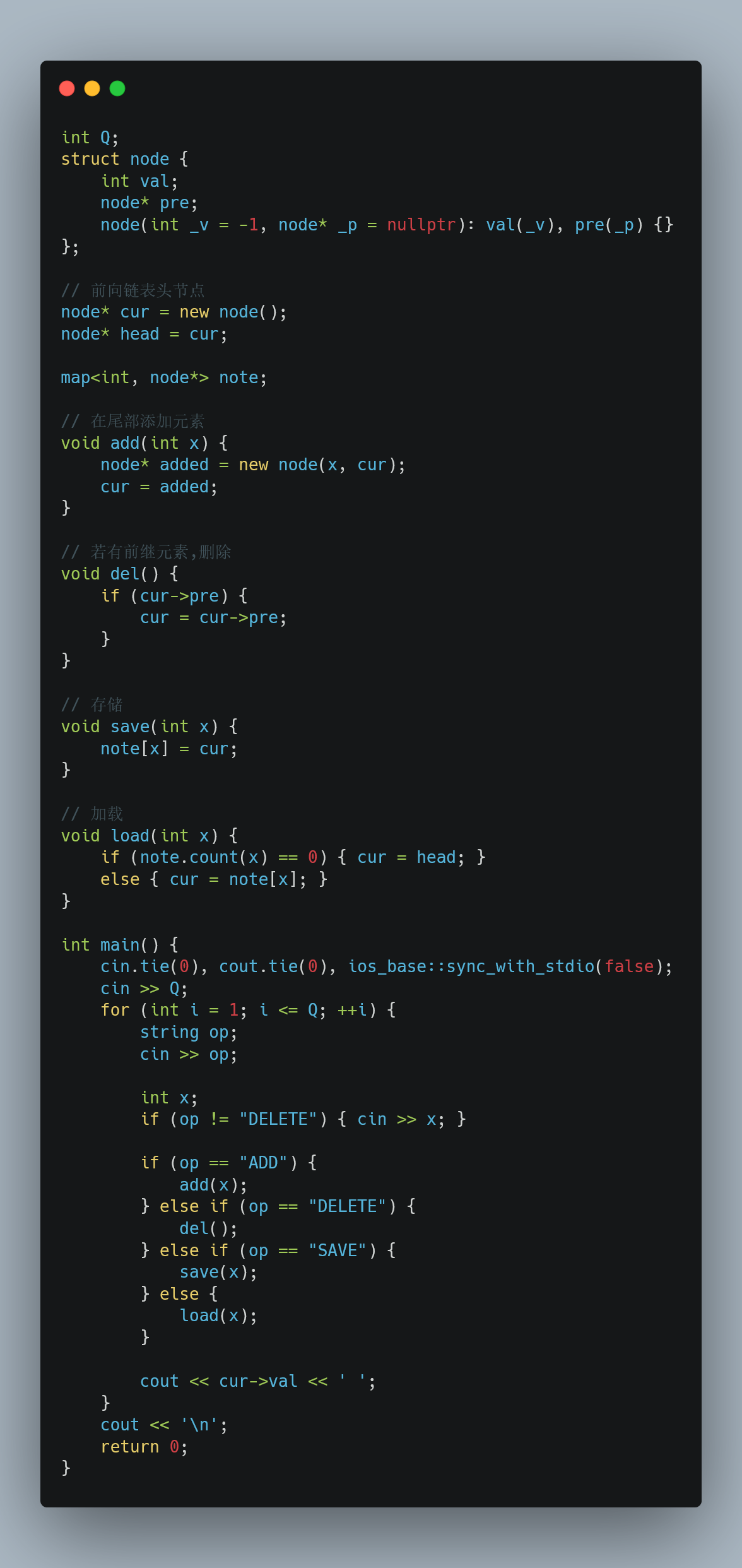
12.22 ABC 273E
https://atcoder.jp/contests/abc273/tasks/abc273_e
一开始你有一个空数组 a 和一个 1e9 页的笔记本,每页上都记录着一个空数组。
有四种类型的操作:
ADD x:在 a 的末尾添加元素 x (1≤x≤1e9)。
DELETE:如果 a 不为空,删除 a 的最后一个元素。
SAVE y:把 a 记在第 y 页上(覆盖原来的数组)。
LOAD z:把 a 替换为第 z 页上的数组。
输入 q(≤5e5) 和 q 个操作。
在每个操作结束后,你需要输出 a 的最后一个元素(数组为空时输出 -1)。
想到前向链表/前缀操作树就很容易实现了(因为我们发现只关心最后一次操作的结果, 之前的数据实际上不需要我们去进行额外的维护, 只要结构可以不断快速的累加, 复制就可以满足条件了)
12.23 ABC 271E
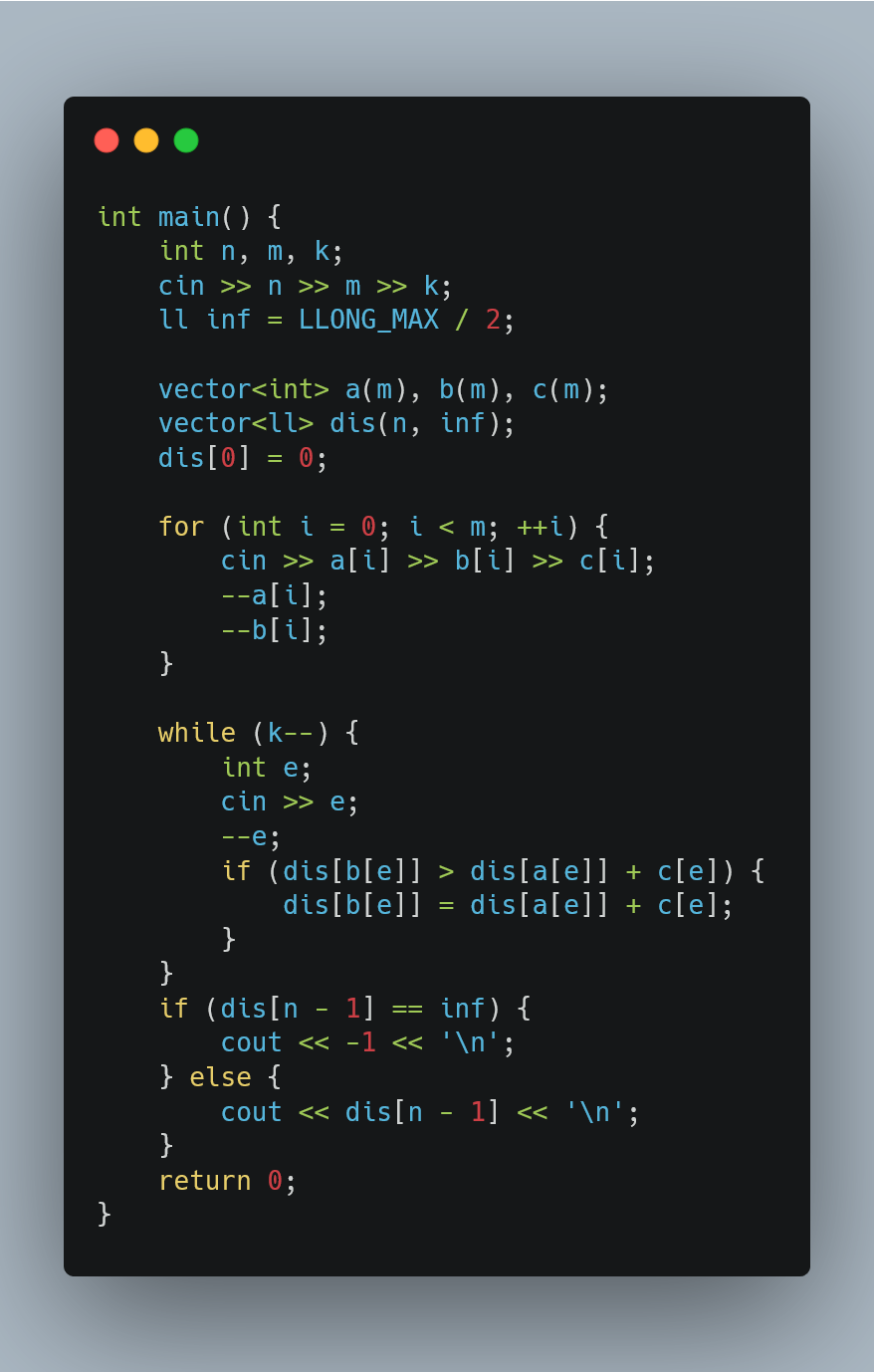
https://atcoder.jp/contests/abc271/tasks/abc271_e
输入 $n,m,k (\leq 2e5)$, 然后输入 $m$ 条边,每条边输入两个点 $x\ y$(表示从 $x$ 到 $y$ 的一条有向边,点的编号 $1-n$ 和一个值在 $[1,1e9]$ 内的边权,每条边的编号 $1-m$
图中没有自环,但可能有重边。
然后输入一个长为 $k$ 的数组 $a (1 \leq e[i] \leq m)$
找到一条从 $1$ 到 $n$ 的路径,满足路径上的边的编号是 $a$ 的子序列
输出满足这个要求的路径的最短长度。如果不存在, 输出 $-1$。
- 找到一条从 $1$ 到 $n$ 的路径, 满足路径上的边的编号是 $a$ 的子序列: 实际上这个条件还是很强的一个约束(必须按照序列的顺序走, 还需要能够到达最终的终点)
- 最短长度 => 通过类似于dijkstra的方式放缩这个序列上的所有边, 加边修改距离, 直到序列内所有的边都被放缩使用过, 观察终点的距离值是否可以到达?
类似于这样的放缩:
1 | for e in seq: |