12.26 ABC 269F

给你一个特殊的矩阵, 每个格子的下标为$(i,j)$, 若$i+j$是一个偶数, 那么这个矩阵格子数值为0, 否则为$i*M + j$, 给你$Q$个查询, 每组查询包含$r_1, r_2, c_1, c_2$;

求 $r_1 \leq r \leq r_2$, $c_1 \leq c \leq c_2$ 之间的所有数字之和.

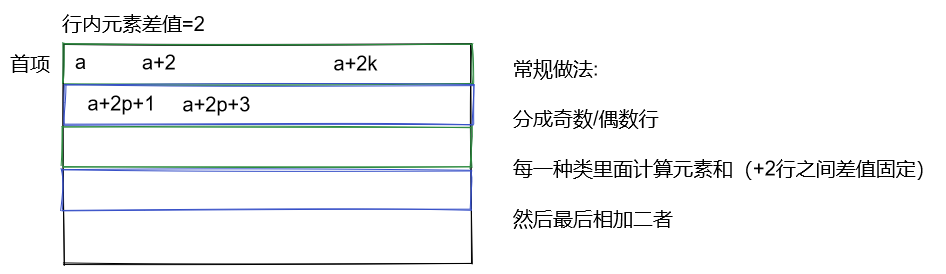
关键:

看出间隔两行之间的和是一个等差数列关系, 公差是固定的.
每一个query都可以看作两组基向量(偶数行, 奇数行)所组成的等差数列, 然后对这两个数列分别求和就可以了.
注意$c_1$还有$c_2$的范围限制, 确定对应的格子内取值, 然后求出单行的数值, 最后套公式求和即可。

12.27 ABC 270F

https://atcoder.jp/contests/abc270/tasks/abc270_f

每一个节点有以下三种选择

在该节点建造港口 $X$
在该节点建造机场 $Y$
在指定两节点间建造一条公路 $(x, y)$ 代价为$z$

处理1,2两种情况 => 建立超级汇点, 让节点与这个虚拟节点连边, 最后两个节点相连 <=> 引入超级节点后这两个节点相连 (通过3直接连接, 或者是通过两次操作1进行连接)

最后考虑使用情况: 1, 2, 12, 不使用12这4种情况都需要考虑, 每一次执行一次至多$2N+M$条边的最小生成树算法, 因此时间复杂度是ok的。

12.28 ABC 268F

https://atcoder.jp/contests/abc268/tasks/abc268_f

邻项交换(假设相邻两项 $P_i$, $P_{i+1}$)
$P_i$ 有$X_i$个X, 数字总和为$Y_i$
$P_{i+1}$ 有$X_{i+1}$个$X$, 数字总和为 $Y_{i+1}$
那么$P_i$放在$P_{i+1}$前面, score = $X_i \times Y_{i+1}$ + ($P_i$内部分数) + ($P_{i+1}$内部的分数)

如果$P_{i+1}$放在$P_i$前面, score = $X_{i+1} \times Y_i$ + ($P_i$内部分数) + ($P_{i+1}$内部的分数)

那么交换更优秀 => $X_i \times Y_{i+1} < X_{i+1} \times Y_i$

所以按照这个顺序排序后得到的结果就是最优秀的，我们按照这个顺序排序并一次求解即可。复杂度就是这一次排序，注意不要爆int了

12.29 ABC 267F

https://atcoder.jp/contests/abc267/tasks/abc267_f

树上两点之间的距离查询问题

给定一颗树和树上的一点u, 问与u距离值为k的点有哪些?

和树的直径有什么关系?

直径端点L和R对应的距离是树上所有点对之间最大的。
只有在范围内部的才有可能存在

因此只需要考虑从直径的端点出发的路径组成, 就能找到这些节点的距离为k的答案节点(因为直径路径是树上最长的路)

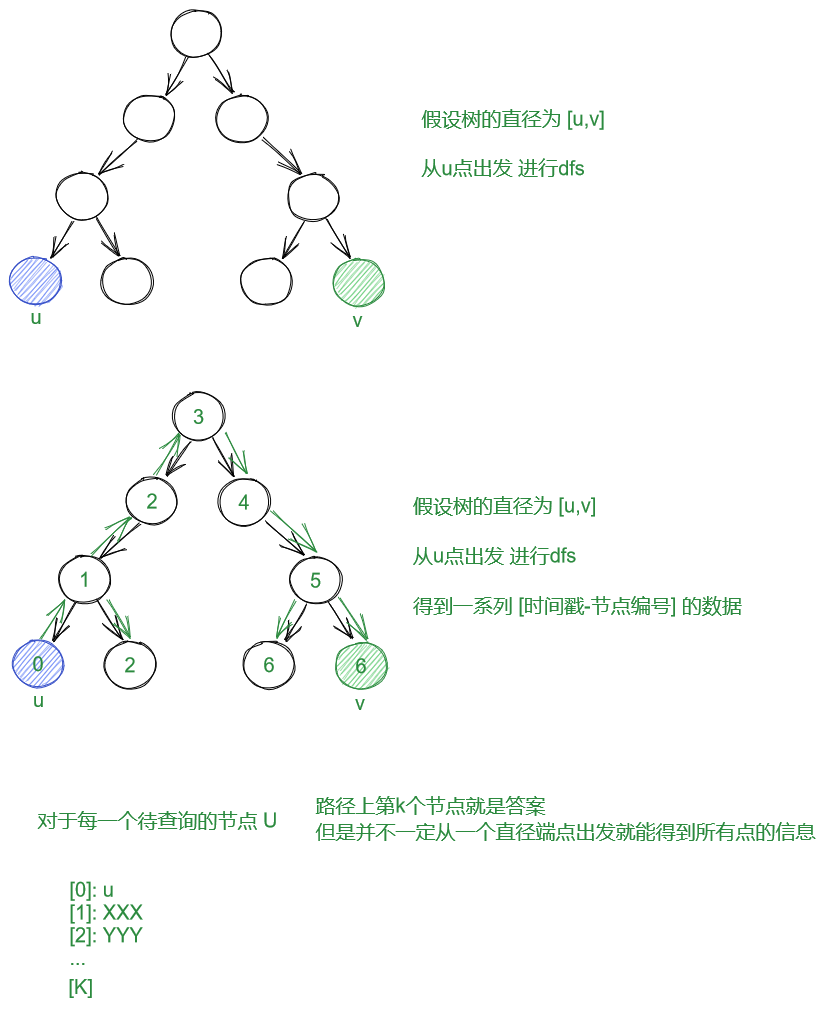
为什么需要从两个端点都走一次?

因为存在一些点, 当我们第一次遍历到的时候, 发现路径长度小于深度k(因此没有答案节点)
但是从另一侧过来就可以满足答案要求的, 所以需要从直径两端各自遍历一次.

12.30 259F Select-Edges

https://atcoder.jp/contests/abc259/tasks/abc259_f

挑选树的边, 满足度数约束的情况下尽可能取得最大值, 求这个最大值;

最大值 => 最优化问题 => 贪心或者 dp
由于存在度数的约束 => 每一条边关联两个端点, 无法简单的按照边权大小贪心 => 会想到dp => 树形dp

树形dp, 特点就是可以按照子树的方式考虑子问题的答案, 然后根据树的特质进而进行状态转移求解。

考虑一个节点$u$, 以及关联$u,v$的一条边, 假设它具有的边权为$w$

如果此时节点$u$, 已经选了一些边, 但是度数大小小于 $d[u] - 1$那么可能需要选这条边, 从而以节点$u$为根的子树的价值就增加 $S[v] + w$; 如果度数达到了上限, 就不选.

假设节点$u$, 有$v_1, v_2, …, v_n$这些节点关联, 那么这些子树挑选哪些会是最好的? 那就是子树权重和(度数未满) + (u,v_i)边的权重 - 不选这条边的最大权重和(v_i度数已经满了)的差值大于0的那些节点. 按照这个顺序排序子树节点, 贪心选取前$d[u]$个(如果差值为负则直接退出)

实现算法的瓶颈在于排序的复杂度, 最终是$O(NlogN)$的.

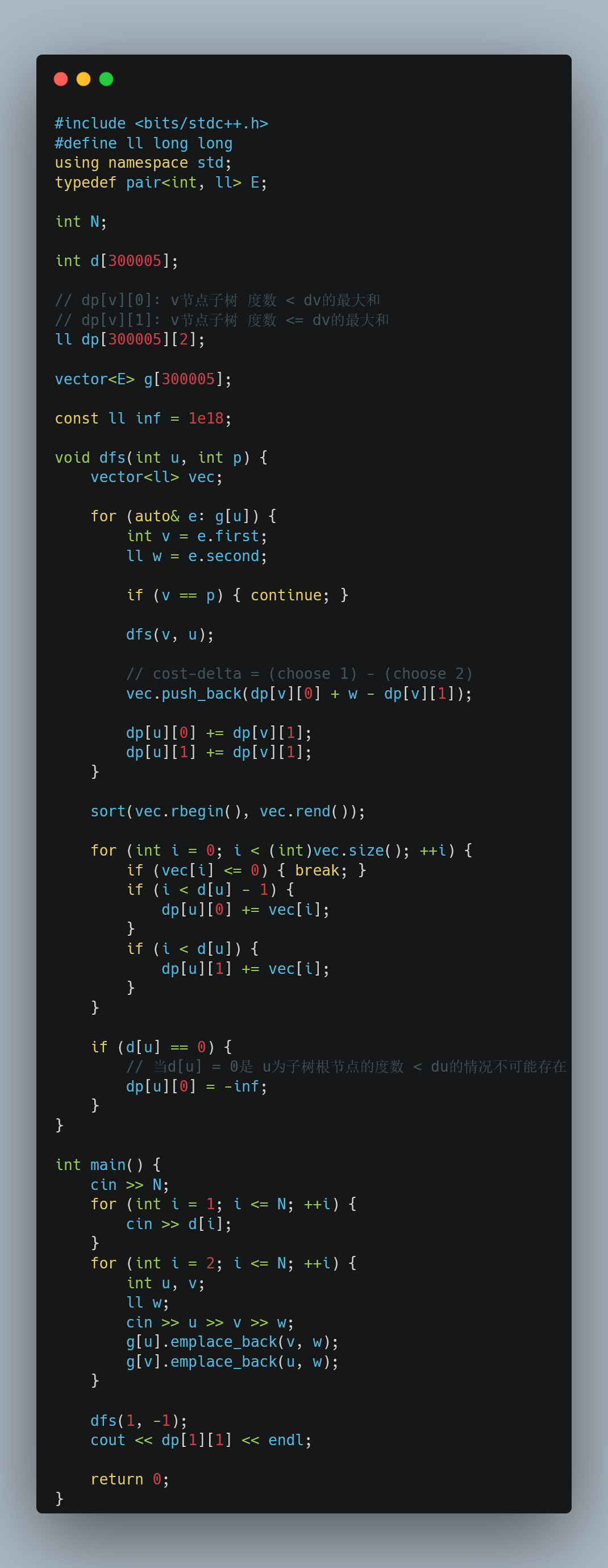
参考实现:

doge的个人site

tea-1226

12.26 ABC 269F

12.27 ABC 270F

12.28 ABC 268F

12.29 ABC 267F

12.30 259F Select-Edges